I have for a long time wanted to write something about the Amiga’s support for line drawing. It’s an area of the Amiga, that’s not so well described out there. This makes it a bit of a challenge, and I lost count on how many times I tried to poke at this stuff.

So why am I doing this? Well, hardware accelerated line drawing was one of the many featues that made the Amiga a superb graphics machine. It’s the prerequisite for everything related to computer generated graphics, like drawing figures and polygons, and also for venturing into the realm of 3D graphics. It all starts with line drawing.

In this three-part series of small posts, we’ll dive into line drawing, from it’s early beginnings, to how it works on Amiga hardware, and finish with a little program written in assembler.

We have reached letter XII of the Amiga Machine Code Course. This final letter is very short on details, so an introduction to line drawing must be found elsewhere - like here!

With that out of the way, let’s get going! 🚀🚀

History

While working at IBM, Jack Elton Bresenham invented an algorithm for drawing lines in 1962, and it’s one of the earliest algorithms in the field of computer graphics. It works by approximating the closest thing to a strait line between two points, using only addition, subtraction, and bit shifting. Those operations are very fast and simple to implement in hardware. This simplicity, was not a result of optional optimization, but a necessity, given the limited hardware back in the day.

Bresenham described his work at the time with these words.

I was working in the computation lab at IBM’s San Jose development lab. A Calcomp plotter had been attached to an IBM 1401 via the 1407 typewriter console. [The algorithm] was in production use by summer 1962, possibly a month or so earlier. Programs in those days were freely exchanged among corporations so Calcomp (Jim Newland and Calvin Hefte) had copies. When I returned to Stanford in Fall 1962, I put a copy in the Stanford comp center library.

The above quote contains a lot of info. Let’s unpack it, and see where it goes.

The IBM 1401 was announced back in 1959 and was a general purpose computer for businesses at an affordable price point. This affordability made it very popular in the early 1960s, with several thousand units sold. That was a lot back then!

In 1959 the system had three units: The 1401 processing unit, the 1402 card reader, and the 1403 text printer. Here’s a promotional picture from back then.

In the picture above, we see a woman pointing at the IBM 1401 processing unit, with her back turned to the 1402 card reader. In the foreground, we see the 1403 text printer. Since the system had no monitor, the printer provided much of the program output to the operator.

Programs were stored on punch cards, which were loaded into the card reader. From there, the program was read into the processing unit, and eventually the program would write it’s output to the printer.

The IBM 1407 console inquiry station, was a table with a typewriter on it, connected to the 1401 and fed continous form paper. The program would write it’s output using the typewriter, and if the program allowed it, the operator could also provide input, by typing it!

However, providing input came at a cost. Since the 1401 did not have an operative system to provide scheduling of jobs, waiting for input could halt the whole system. In todays money, the 1401 system would cost 10 dollars a minute to rent. 😱

Shortly after the release of the 1401 system, the enevitable happened. People began tinkering with computer graphics, but the 1403 printer left something to be desired. Here we see an output from the program Sophie 😉.

Obviously, there was a demand for better graphics output devices, and one of the first, was the Calcomp 565 drum plotter, also marketed by IBM as the IBM 1627.

Here’s a video of the plotter in action. It’s noisy and build like a tank!

Thanks to the 1401 revival project, over at the Computer History Musuem, a complete IBM 1401 data center has been recreated, so that we can get a climpse of how this system works. 👍

Bresenham never did patent his algorithm, and it was exchanged freely among peers at the time. In fact a very early version of his code, for the IBM 1440 system, a lower cost version of the IBM 1401, can be found over at bitsavers.org. The code mentions the IBM 1447 - a physical console, which was part of the 1440 system.

I hope that this little trip into computer history, has given a better understanding of the system Bresenham worked on. It’s amazing just how limited the hardware was back then, and Bresenham could not have made his algorithm, without considering these limitations.

Today, we have so much computing power, that it’s hard to walk in the footsteps of Bresenham. Many of the tricks he used, have long been forgotten by most, and are today relegated to obscurity, or confined to the black arts of programming. 😉

Anyways, it could be interesting to retrace the steps, that I guess, Bressenham must have taken. We start with something naive, and perform some tweaks along the way. The goal is a line drawing algorithm, that avoids any expensive multiplication, division, and floating point operations.

Let’s Draw a Line

The equation for a line look like this. $$ y = ax + b$$

Now, let’s say the line is drawn between the two points $(x_1, y_1)$ and $(x_2, y_2)$, then we can define the distances $\Delta x = x_2 - x_1$ and $\Delta y = y_2 - y_1$, and calculate the gradient $a$.

$$a = \frac{\Delta y}{\Delta x}$$

And then we solve for $(x_1, y_1)$, and find $b$ $$b = y_1 - \frac{\Delta y}{\Delta x} x_1$$

To keep things simple, we want the gradient to only assume positive values. We do this by adding constraints; let’s say $0 \leq x_1 \lt x_2$ and $0 \leq y_1 \leq y_2$, which gives us a gradient $a \geq 0$. Last, but not least, both $x$ and $y$ should be integers.

Let’s start by making a naive algorithm to draw a line.

void naiveLineDraw(int x1, int y1, int x2, int y2) {
  int dx = x2 - x1;
  int dy = y2 - y1;

  float a = (float) dy / dx;
  float b = y1 - a * x1;  
  
  plot(x1,y1)
  
  while (x1 < x2) {
    x1 += 1
    y1 = Math.round( a * x1 + b );
    plot(x1,y1)
  }
}

For readability I omitted various checks - like checking for division by zero or drawing outside the screen. The rounding method rounds to the nearest integer.

The naive algorithm calls a plot function, that delivers an output in pixels, like the one shown below for a line between the points $(1,1)$ and $(11,5)$ with the green squares as pixels.

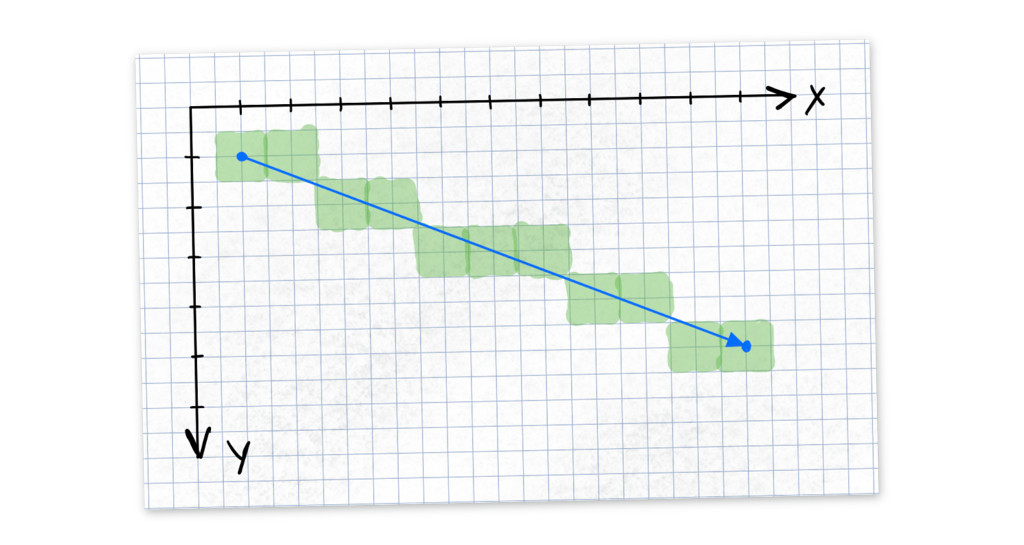
The $y$ axis points downward, a typical thing in computer graphics, and the pixels are defined by their midpoint. The blue arrow is the true line.

Well, that seems to work quite well, so are we done yet?

Not quite, there’s one more problem with the naive algorithm. It has to do with the gradient $a$. When it becomes larger than one, holes starts to appear in our line. E.g. try to use the naive algorithm on the two points $(1,1)$ and $(3,5)$.

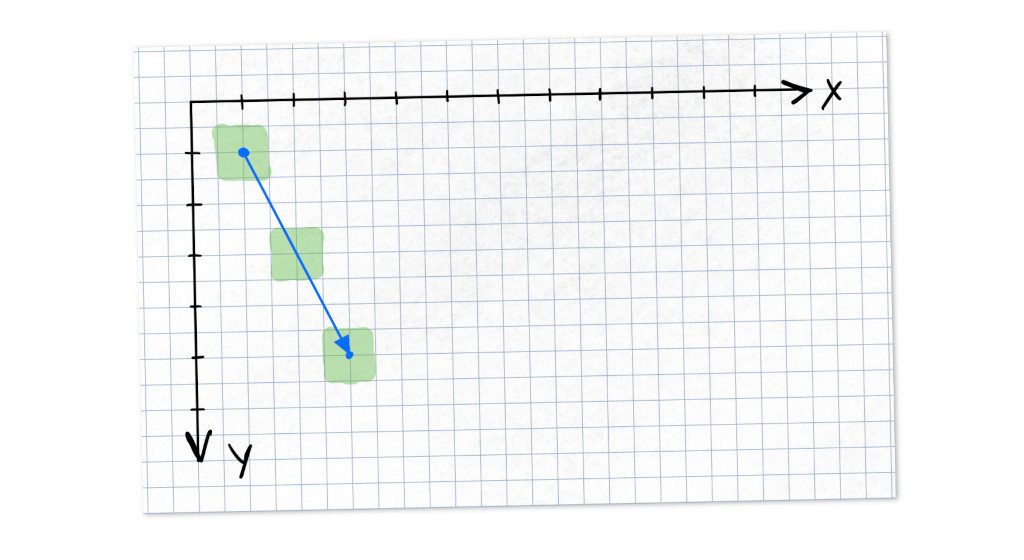
To avoid the holes, $y$ must not be incremented by more than $1$, and the only way to ensure this, is by introducing a new constraint on the gradient $a$.

$$0 \leq a \leq 1$$

So, let’s revist our constraints

$$ 0 \leq x_1 < x2 \Rightarrow \Delta x \gt 0$$ $$ 0 \leq y_1 \leq y2 \Rightarrow \Delta y \geq 0 $$ and because $$ 0 \leq a = \frac{\Delta y}{\Delta x} \leq 1$$ it follows that $$ \Delta y \leq \Delta x$$

Now that we have our constraints in place, the next step is to optimize the code.

Optimizations

The naive algorithm has some issues, especially for old machines, like the IBM 1440, but also for an Amiga 500. The performance hit comes from the division and the multiple multiplications. The use of floating point numbers, are not trivial either, since the 68K CPU does not have an FPU 😱.

We need to get rid of the floating point types, the division, and the multiplications. It all comes together in the rouding function, so let’s start by doing something about that.

y1 = Math.round( a * x1 + b );

The rounding function rounds the input to the nearest integer. If the fractional part of the input is below $0.5$, it rounds down, otherwise it rounds up.

It’s easy to emulate that behaviour by adding $0.5$ and using the integer part of the result.

y1 = (int) (a * x1 + b + 0.5);

The cast to an integer indicates that it’s the integer part of the evaluated expression that is stored. It’s basically a truncation, where we strip the result of it’s fractional part.

The above expression has the advantage, that we can come with any $x_1$ and get a $y_1$, but that flexability is not needed. Since $x_1$ is always incremented by one, we can use an incremental calculation instead.

We know that

$$y_n = ax_n + b$$ $$y_{n+1} = ax_{n+1} + b$$

Let’s change the calculation of $y$ to use a difference equation.

$$y_{n+1} - y_{n} = a (x_{n+1} - x_{n})$$

Since each iteration increment $x$ by one, we can further reduce this to

$$y_{n+1} - y_{n} = a$$

And voila, we have a new expression for the next $y$ 👍

$$y_{n+1} = y_{n} + a$$

A nice side effect of the incremental calculation, is that we eliminated the floating point $b$ in the process. Now, let’s see what we can do about $a$.

The rounding effect of $0.5$ is not part of the difference equation, but we must add it somehow. We can’t add it to the initial $y_1$, outside the while loop, because $y_1$ is an integer.

y1 += 0.5 + a;  // compile error

There’s also a problem in the while loop, because $a$ is a floating point.

// inside the while loop
y1 += (int) (a); // won't work

Updating $y_1$ by truncating $a$ to an integer won’t work. When $a < 1$ the truncated integer value will become zero, and $y_1$ will never increase.

Previously we prevented holes in the line, by only letting $y$ increase by no more than one. Let’s use that, to introduce a floating point accumulator, that we contionously update in the while loop.

float accumulator = 0.5 + a;

// inside the while loop
if (accumulator < 1) {
  accumulator += a;
} else {
  y1 += 1;
  accumulator += a - 1
}

We know that the true line is increased with the gradient $a$, when we increment $x$ by one. We express this in the accumulator, by increasing it with $a$ at every iteration.

When the accumulator becomes larger than one, we know that the true line has moved so much, that we can increment $y_1$ with one pixel. And because we do this, we also need to subtract one from the accumulator.

The accumulator can be changed to an integer, without loosing precision. Let’s start by looking at the value of the accumulator, the first time we draw a pixel.

$$\textrm{accumulator} = 0.5 + a = 0.5 + \frac{\Delta y}{\Delta x}$$

We can get rid of the expensive division by multiplying with $2\Delta x$, which yields an equivalent accumulator.

$$\textrm{accumulator} = \Delta x + 2 \Delta y$$

The accumulator is now an integer 😃. We need to update the algorithm also.

// multiplying with 2*dx
int accumulator = dx + 2*dy;

// inside the while loop
if (accumulator < 2*dx) {
  accumulator += 2*dy;
} else {
  y1 += 1;
  accumulator += 2*(dy - dx)
}

We can make the if-check simpler by subtracting $2\Delta x$ from the initial accumulator.

// subtracting 2*dx
int accumulator = 2*dy - dx;

// inside the while loop
if (accumulator < 0) {
  accumulator += 2*dy;
} else {
  y1 += 1;
  accumulator += 2*(dy - dx)
}

The floating point numbers are now gone, the division is gone, and the multiplications can be replaced by bit shifting. This has become a usable algorithm! 🚀

The new and better algorithm look like this (I kept the multiplications for readability, but they should be replaced by a single left shift).

void betterLineDraw(int x1, int y1, int x2, int y2) {
  int dx = x2 - x1;
  int dy = y2 - y1;  
  plot(x1,y1)
  int accumulator = 2*dy - dx;
  
  while (x_1 < x2) {
    x1 += 1
    if (accumulator < 0) {
      accumulator += 2*dy;
    } else {
      y1 += 1;
      accumulator += 2*(dy - dx)
    }           
    plot(x1,y1)
  }
}

If we try out the better line draw algorithm on a gradient less than zero or larger than one, it won’t work. It’s also quite sensitive to the order of the endpoints. It can draw a line between the points $(1,1)$ and $(11,5)$, but not the other way around. That’s not very usable, so the algorithm has to be extended with the concept of octants.

The Octants

A correct implementation of Breseneham’s line algorithm, must of course be able to plot lines in all directions. The better line draw algorihthm only works in one region, also known as an octant. An octant is relative to the line starting position and spans an angle of 45 degrees, and it takes eight of them to cover all 360 degrees.

It turns out that if you can draw a line in one octant, then you can draw a line in all directions, due to symetries between octants.

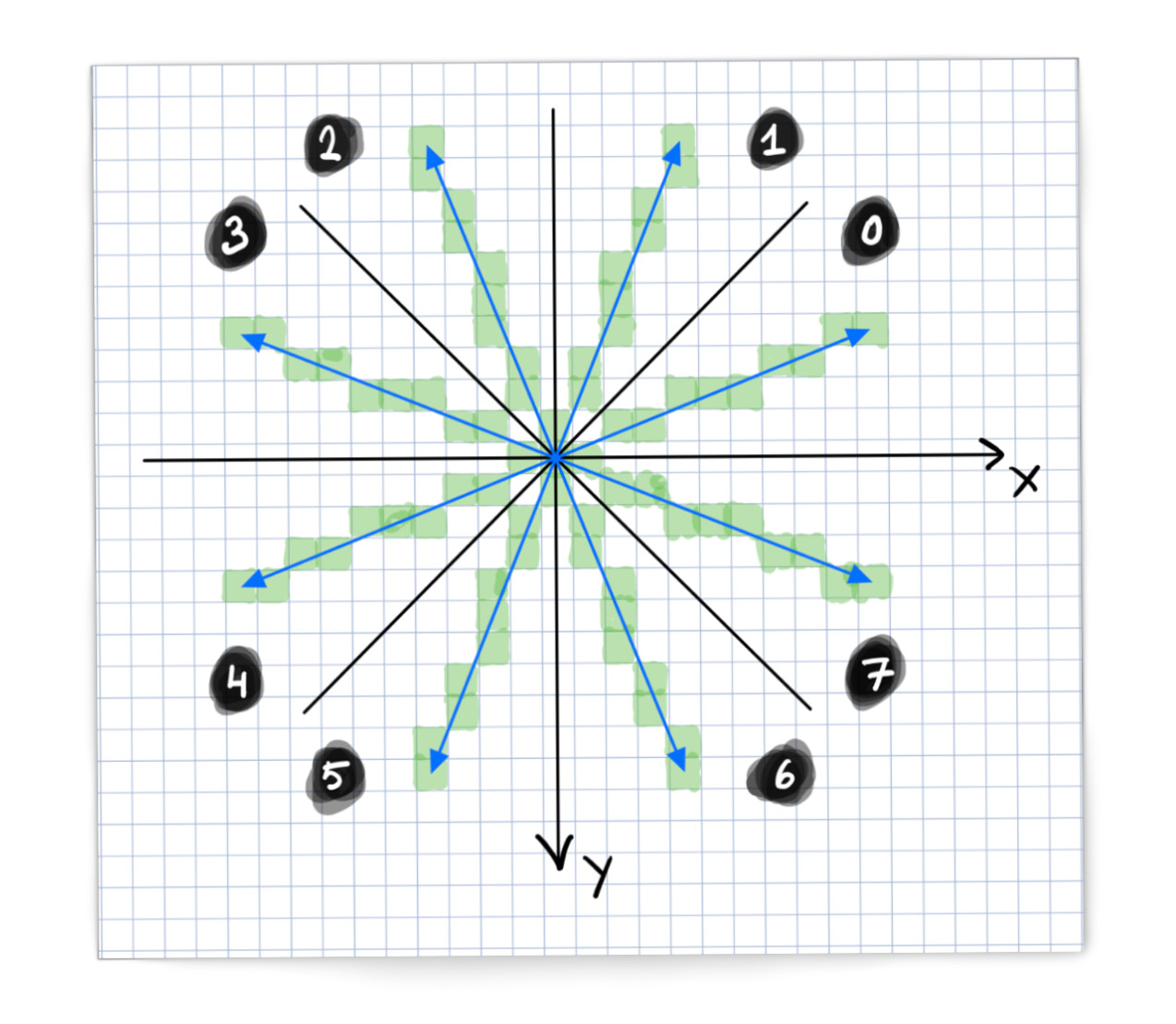
The better line draw algorithm can only draw lines in octant 7, so it must be tweaked a bit to be generalized to all octants.

More Than Just Line Drawing

When I first started looking at Bresenham’s algorithm, I thought it only could be used for line drawing. But it turns out it applies to a much wider scope, even things I would never have thought of. Here’s a couple of examples.

Bresenham’s algorithm can be used to do evenly-spaced sampling. Let’s say we want to pick 7 evenly-spaced samples from an array containing the integers from 0 to 999. Bresenham algorithm gives us something distributed as evenly as possible.

$$[0, 167, 333, 500, 666, 833, 999] $$

Another use-case for Bresenham’s algorithm is to make smooth color fades. Here’s an example from the game Petris.

And here’s one of my favorites. Bresenham’s algorithm can also be used to distribute evenly for euclidian rythms. 🥁

It’s amazing how well euclidiean rythms sounds, especially when Bresenham’s algorithm can’t quite distribute equally. Instead it yields something as evenly as possible, which adds syncopations, small disturbances or interruptions, to the regular flow of the rythm. Funky stuff indeed!

Part 2 of this post is going to focus on how the Amiga implements Bresenham’s algorithm in hardware. Stay tuned 😃 🚀

---

Amiga Machine Code Course

Previous post: Amiga Machine Code Letter XII - Horizontal Sine Shifting

Next post: Amiga Machine Code Letter XII - Line Drawing 2