Amiga Machine Code Letter VI - Blitter

Mar 2, 2019 6 min read

Amiga Machine Code - Letter VI - Blitter

We have reached Letter VI of the Amiga Machine Code course. I will only skip through the details in this post. Make sure to read the letter, to get a grasp of things.

The main theme of this letter, is moving bytes from an array of memory to another. In the Amiga this can be done with hardware support, through a technique called blitting.

The word blitting is derived from the BitBLT routine for the Xerox Alto computer in connection with Smalltalk, and stands for bit block transfer.

By using a combination of custom chip registers, it’s possible to point out arrays of memory that should be transfered to another part of memory - typically the screen memory.

Moving data could be a CPU intensive task, but not in the Amiga. Blitting is handled by the Agnus chipset, which allows for fast transfer of memory without involving the 68K CPU.

The concept of blitting is different from sprites. While sprites are stored seperate from screen memory, blitting writes directly to screen memory.

The Amiga has three memory sources $A$, $B$, and $C$, that can be combinded using a boolean function, and written to the memory destination $D$.

Blitting is controlled by the BLTCON0 and BLTCON1 control registers, which also defines the boolean transfer function.

The memory areas $A$, $B$, $C$, and $D$ are defined by giving pointers to the BLTxPTH / BLTxPTL control registers.

Similarly, the modulus for each source is controlled by the BLTxMOD control registers. The modulus is given in bytes.

Finally, the size of the blitter, in width and height, is set by the BLTSIZE control register. The height is given in lines, and the width in words (16 pixels).

Given a screen with 40 bytes of width, and a blitter area of width 4 words, the modulus is:

$40 bytes - ( 4 words * 2 ) = ( 40 - 8 ) bytes = 32 bytes$

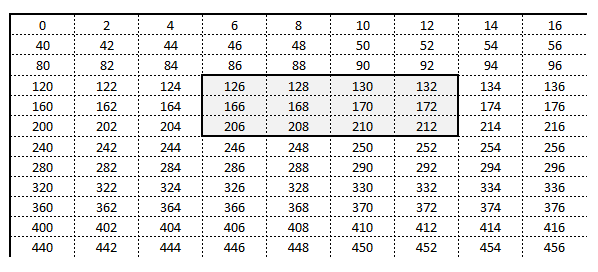
In the image below, we can see the situation visualized. When the blitter reaches offset 134 from the start of screen memory, it adds the modulus of 32 bytes to get to the next memory address to blit, which in this case is 134 + 32 = 166.

Blitter memory

Function Generator

The three bitplanes $A$, $B$, and $C$ can be combined using a boolean function, before beeing written to the destination $D$. This boolean function is defined by the lower byte in the BLTCON0 register. There is a writeup about it, in the Amiga Hardware Reference Manual.

The function generator is quite engineous in it’s simplicity. It uses so-called minterms, that enables any boolean function of $A$, $B$, and $C$ to be written as a sum of minterms.

pos	$A$	$B$	$C$	$D$	Minterm
0	0	0	0	?	$\overline{ABC}$
1	0	0	1	?	$\overline{AB}C$
2	0	1	0	?	$\overline{A}B\overline{C}$
3	0	1	1	?	$\overline{A}BC$
4	1	0	0	?	$A\overline{BC}$
5	1	0	1	?	$A\overline{B}C$
6	1	1	0	?	$AB\overline{C}$
7	1	1	1	?	$ABC$

There is a great insight in this simplicity, that makes the function generator really beautiful in it’s design. All of this is made possible by simple boolean algebra, where every part of an expression can be turned into a minterm, by using the following rule

$1 = A + \overline{A} = B + \overline{B} = C + \overline{C}$

Let’s use this insight to expand the following expression into it’s equivalent minterms.

$ \begin{split} D & = A\overline{C} + B \\\
& = A(1)\overline{C} + (1)B(1) \\\
& = A(B+\overline{B})\overline{C} + (A + \overline{A})B(C + \overline{C}) \\\
& = AB\overline{C} + A\overline{BC} + ABC + AB\overline{C} + \overline{A}BC + \overline{A}B\overline{C} \\\
& = AB\overline{C} + A\overline{BC} + ABC + \overline{A}BC + \overline{A}B\overline{C} \\\
\end{split} $

Looking up each of the five minterms in the table, reveals that we have to set bit 6, 4, 7, 3, and 2 of the BLTCON0 register, which corresponds to setting the lower byte to %11011100 = $dc.

The above method, is a rather cumbersome way of setting the function generator, so both Letter VI and the Amiga Hardware Reference Manual offers a quicker alternative, using precalculated minterms.

Expression	BLTCON0 LF	Expression	BLTCON0 LF
$D = A$	$f0	$D = AB$	$c0
$D = \overline{A}$	$0f	$D=A\overline{B}$	$30
$D = B$	$cc	$D=\overline{A}B$	$0c
$D=\overline{B}$	$33	$D=\overline{AB}$	$03
$D=C$	$aa	$D=BC$	$88
$D=\overline{C}$	$55	$D=B\overline{C}$	$44
$D=AC$	$a0	$D=\overline{B}C$	$22
$D=A\overline{C}$	$50	$D=\overline{BC}$	$11
$D=\overline{A}C$	$0a	$D=A+\overline{B}$	$f3
$D=\overline{AC}$	$05	$D=\overline{A+B}$	$3f
$D=A+B$	$fc	$D=A+\overline{C}$	$f5
$D=\overline{A}+B$	$cf	$D=\overline{A+C}$	$5f
$D=A+C$	$fa	$D=B+\overline{C}$	$dd
$D=\overline{A}+C$	$af	$D=\overline{B+C}$	$77
$D=B+C$	$ee	$D = AB + \overline{A}C$	$ca
$D=\overline{B}+C$	$bb	$D=A\overline{B} + AC$	$ac

We can quickly assure ourself that the precalculated minterms allows for a faster process. If we consider the example from before.

$ \begin{split} D &= A\overline{C} + B \\\
A\overline{C} &= \$50 &= \%01010000 \\\
B &= \$cc &= \underline{\%11001100} \\\
A\overline{C} + B &= \$dc &= \%11011100 \end{split} $

We arive at the result by looking up each term in the precalculated table. Then use an or (because of the $+$) to get the final result.

If it’s hard to see why the boolean function generator is useful, then read the car animation example in the Amiga Hardware Reference Manual.

The blitter would be much less useful if it was not for it’s boolean function generator. By carefully setting up a boolean function, the blitter can be used to move objects around on the screen, in much the same way as sprites.

However, blitter objects, or bob’s as they are called, are written directly to screen memory, as opposed to sprites that are stored in their own memory. This requires that the background is countionusly redrawn as part of the blit.

To illustrate, I have found a graphics test by Master484, that uses blitter objects in a Street Fighter game.

Street Fighter

In the above screenshot, the sumo wrestler is blitted into the screen. But since blitter can only draw a rectangular area, we also have to draw the background as part of the blit. This is where the boolean function generator excels.

Let’s define memory where the sumo wrestler is as $B$ and a corresponding mask as $A$, and the background as $C$. When ever the mask is set, we pass through the wrestler data, and when the mask is not set, we pass through the background. This is exactly what the cookie-cut function does.

$D = AB + \overline{A}C$

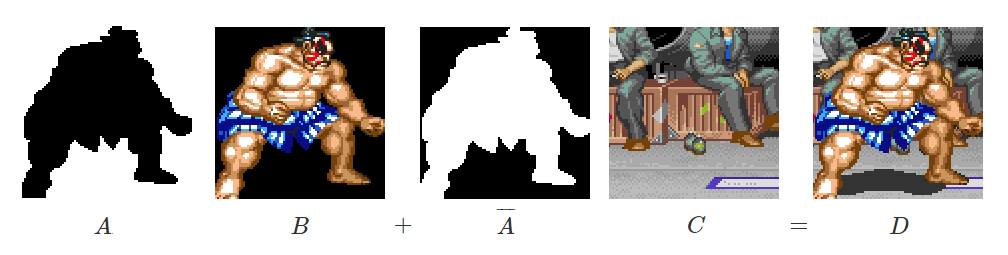
cookie-cut